
Pythagorean Mathematics

CONCERNING the secret significance of numbers there has been much speculation. Though many interesting discoveries have been made, it may be safely said that with the death of Pythagoras the great key to this science was lost. For nearly 2500 years philosophers of all nations have attempted to unravel the Pythagorean skein, but apparently none has been successful.
Notwithstanding attempts made to obliterate all records of the teachings of Pythagoras, fragments have survived which give clues to some of the simpler parts of his philosophy. The major secrets were never committed to writing, but were communicated orally to a few chosen disciples. These apparently dated not divulge their secrets to the profane, the result being that when death sealed their lips the arcana died with diem.
Certain of the secret schools in the world today are perpetuations of the ancient Mysteries, and although it is quite possible that they may possess some of the original numerical formulæ, there is no evidence of it in the voluminous writings which have issued from these groups during the last five hundred years. These writings, while frequently discussing Pythagoras, show no indication of a more complete knowledge of his intricate doctrines than the post-Pythagorean Greek speculators had, who talked much, wrote little, knew less, and concealed their ignorance under a series of mysterious hints and promises. Here and there among the literary products of early writers are found enigmatic statements which they made no effort: to interpret. The following example is quoted from Plutarch:
"The Pythagoreans indeed go farther than this, and honour even numbers and geometrical diagrams with the names and titles of the gods. Thus they call the equilateral triangle head-born Minerva and Tritogenia, because it may be equally divided by three perpendiculars drawn from each of the angles. So the unit they term Apollo, as to the number two they have affixed the name of strife and audaciousness, and to that of three, justice. For, as doing an injury is an extreme on the one side, and suffering one is an extreme on the on the one side, and suffering in the middle between them. In like manner the number thirty-six, their Tetractys, or sacred Quaternion, being composed of the first four odd numbers added to the first four even ones, as is commonly reported, is looked upon by them as the most solemn oath they can take, and called Kosmos." (Isis and Osiris.)
Earlier in the same work, Plutarch also notes: "For as the power of the triangle is expressive of the nature of Pluto, Bacchus, and Mars; and the properties of the square of Rhea, Venus, Ceres, Vesta, and Juno; of the Dodecahedron of Jupiter; so, as we are informed by Eudoxus, is the figure of fifty-six angles expressive of the nature of Typhon." Plutarch did not pretend to explain the inner significance of the symbols, but believed that the relationship which Pythagoras established between the geometrical solids and the gods was the result of images the great sage had seen in the Egyptian temples.
Albert Pike, the great Masonic symbolist, admitted that there were many points concerning which he could secure no reliable information. In his Symbolism, for the 32° and 33°, he wrote: "I do not understand why the 7 should be called Minerva, or the cube, Neptune." Further on he added: "Undoubtedly the names given by the Pythagoreans to the different numbers were themselves enigmatical and symbolic-and there is little doubt that in the time of Plutarch the meanings these names concealed were lost. Pythagoras had succeeded too well in concealing his symbols with a veil that was from the first impenetrable, without his oral explanation * * *."
This uncertainty shared by all true students of the subject proves conclusively that it is unwise to make definite statements founded on the indefinite and fragmentary information available concerning the Pythagorean system of mathematical philosophy. The material which follows represents an effort to collect a few salient points from the scattered records preserved by disciples of Pythagoras and others who have since contacted his philosophy.
METHOD OF SECURING THE NUMERICAL POWER OF WORDS
The first step in obtaining the numerical value of a word is to resolve it back into its original tongue. Only words of Greek or Hebrew derivation can be successfully analyzed by this method, and all words must be spelled in their most ancient and complete forms. Old Testament words and names, therefore, must be translated back into the early Hebrew characters and New Testament words into the Greek. Two examples will help to clarify this principle.
The Demiurgus of the Jews is called in English Jehovah, but when seeking the numerical value of the name Jehovah it is necessary to resolve the name into its Hebrew letters. It becomes יהוה, and is read from right to left. The Hebrew letters are: ה, He; ו, Vau; ה, He; י, Yod; and when reversed into the English order from left to right read: Yod-He-Vau-He. By consulting the foregoing table of letter values, it is found that the four characters of this sacred name have the following numerical significance: Yod equals 10. He equals 5, Vau equals 6, and the second He equals 5. Therefore, 10+5+6+5=26, a synonym of Jehovah. If the English letters were used, the answer obviously would not be correct.
The second example is the mysterious Gnostic pantheos Abraxas. For this name the Greek table is used. Abraxas in Greek is Ἀβραξας. Α = 1, β = 2, ρ = 100, α = 1, ξ =60, α = 1, ς = 200, the sum being 365, the number of days in the year. This number furnishes the key to the mystery of Abraxas, who is symbolic of the 365 Æons, or Spirits of the Days, gathered together in one composite personality. Abraxas is symbolic of five creatures, and as the circle of the year actually consists of 360 degrees, each of the emanating deities is one-fifth of this power, or 72, one of the most sacred numbers in the Old Testament of the Jews and in their Qabbalistic system. This same method is used in finding the numerical value of the names of the gods and goddesses of the Greeks and Jews.
All higher numbers can be reduced to one of the original ten numerals, and the 10 itself to 1. Therefore, all groups of numbers resulting from the translation of names of deities into their numerical equivalents have a basis in one of the first ten numbers. By this system, in which the digits are added together, 666 becomes 6+6+6 or 18, and this, in turn, becomes 1+8 or 9. According to Revelation, 144,000 are to be saved. This number becomes 1+4+4+0+0+0, which equals 9, thus proving that both the Beast of Babylon and the number of the saved refer to man himself, whose symbol is the number 9. This system can be used successfully with both Greek and Hebrew letter values.
The original Pythagorean system of numerical philosophy contains nothing to justify the practice now in vogue of changing the given name or surname in the hope of improving the temperament or financial condition by altering the name vibrations.
There is also a system of calculation in vogue for the English language, but its accuracy is a matter of legitimate dispute. It is comparatively modern and has no relationship either to the Hebrew Qabbalistic system or to the Greek procedure. The claim made by some that it is Pythagorean is not supported by any tangible evidence, and there are many reasons why such a contention is untenable. The fact that Pythagoras used 10 as the basis of calculation, while this system uses 9--an imperfect number--is in itself almost conclusive. Furthermore, the arrangement of the Greek and Hebrew letters does not agree closely enough with the English to permit the application of the number sequences of one language to the number sequences of the others. Further experimentation with the system may prove profitable, but it is without basis in antiquity. The arrangement of the letters and numbers is as follows:
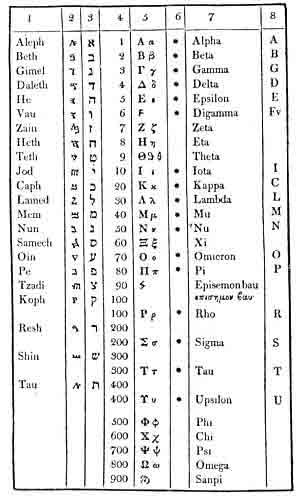
THE NUMERICAL VALUES OF THE HEBREW, GREEK, AND SAMARITAN ALPHABETS.
The letters under each of the numbers have the value of the figure at: the top of the column. Thus, in the word man, M = 4, A = 1, N = 5: a total of 10. The values of the numbers are practically the same as those given by the Pythagorean system.
AN INTRODUCTION TO THE PYTHAGOREAN THEORY OF NUMBERS
(The following outline of Pythagorean mathematics is a paraphrase of the opening chapters of Thomas Taylor's Theoretic Arithmetic, the rarest and most important compilation of Pythagorean mathematical fragments extant.)
The Pythagoreans declared arithmetic to be the mother of the mathematical sciences. This is proved by the fact that geometry, music, and astronomy are dependent upon it but it is not dependent upon them. Thus, geometry may be removed but arithmetic will remain; but if arithmetic be removed, geometry is eliminated. In the same manner music depends upon arithmetic, but the elimination of music affects arithmetic only by limiting one of its expressions. The Pythagoreans also demonstrated arithmetic to be prior to astronomy, for the latter is dependent upon both geometry and music. The size, form, and motion of the celestial bodies is determined by the use of geometry; their harmony and rhythm by the use of music. If astronomy be removed, neither geometry nor music is injured; but if geometry and music be eliminated, astronomy is destroyed. The priority of both geometry and music to astronomy is therefore established. Arithmetic, however, is prior to all; it is primary and fundamental.
Pythagoras instructed his disciples that the science of mathematics is divided into two major parts. The first is concerned with the multitude, or the constituent parts of a thing, and the second with the magnitude, or the relative size or density of a thing.
Magnitude is divided into two parts--magnitude which is stationary and magnitude which is movable, the stationary pare having priority. Multitude is also divided into two parts, for it is related both to itself and to other things, the first relationship having priority. Pythagoras assigned the science of arithmetic to multitude related to itself, and the art of music to multitude related to other things. Geometry likewise was assigned to stationary magnitude, and spherics (used partly in the sense of astronomy) to movable magnitude. Both multitude and magnitude were circumscribed by the circumference of mind. The atomic theory has proved size to be the result of number, for a mass is made up of minute units though mistaken by the uninformed for a single simple substance.
Owing to the fragmentary condition of existing Pythagorean records, it is difficult to arrive at exact definitions of terms. Before it is possible, however, to unfold the subject further some light must he cast upon the meanings of the words number, monad, and one.
The monad signifies (a) the all-including ONE. The Pythagoreans called the monad the "noble number, Sire of Gods and men." The monad also signifies (b) the sum of any combination of numbers considered as a whole. Thus, the universe is considered as a monad, but the individual parts of the universe (such as the planets and elements) are monads in relation to the parts of which they themselves are composed, though they, in turn, are parts of the greater monad formed of their sum. The monad may also be likened (c) to the seed of a tree which, when it has grown, has many branches (the numbers). In other words, the numbers are to the monad what the branches of the tree are to the seed of the tree. From the study of the mysterious Pythagorean monad, Leibnitz evolved his magnificent theory of the world atoms--a theory in perfect accord with the ancient teachings of the Mysteries, for Leibnitz himself was an initiate of a secret school. By some Pythagoreans the monad is also considered (d) synonymous with the one.
Number is the term applied to all numerals and their combinations. (A strict interpretation of the term number by certain of the Pythagoreans excludes 1 and 2.) Pythagoras defines number to be the extension and energy of the spermatic reasons contained in the monad. The followers of Hippasus declared number to be the first pattern used by the Demiurgus in the formation of the universe.
The one was defined by the Platonists as "the summit of the many." The one differs from the monad in that the term monad is used to designate the sum of the parts considered as a unit, whereas the one is the term applied to each of its integral parts.
There are two orders of number: odd and even. Because unity, or 1, always remains indivisible, the odd number cannot be divided equally. Thus, 9 is 4+1+4, the unity in the center being indivisible. Furthermore, if any odd number be divided into two parts, one part will always be odd and the other even. Thus, 9 may be 5+4, 3+6, 7+2, or 8+1. The Pythagoreans considered the odd number--of which the monad was the prototype--to be definite and masculine. They were not all agreed, however, as to the nature of unity, or 1. Some declared it to be positive, because if added to an even (negative) number, it produces an odd (positive) number. Others demonstrated that if unity be added to an odd number, the latter becomes even, thereby making the masculine to be feminine. Unity, or 1, therefore, was considered an androgynous number, partaking of both the masculine and the feminine attributes; consequently both odd and even. For this reason the Pythagoreans called it evenly-odd. It was customary for the Pythagoreans to offer sacrifices of an uneven number of objects to the superior gods, while to the goddesses and subterranean spirits an even number was offered.
Any even number may be divided into two equal parts, which are always either both odd or both even. Thus, 10 by equal division gives 5+5, both odd numbers. The same principle holds true if the 10 be unequally divided. For example, in 6+4, both parts are even; in 7+3, both parts are odd; in 8+2, both parts are again even; and in 9+1, both parts are again odd. Thus, in the even number, however it may be divided, the parts will always be both odd or both even. The Pythagoreans considered the even number-of which the duad was the prototype--to be indefinite and feminine.
The odd numbers are divided by a mathematical contrivance--called "the Sieve of Eratosthenes"--into three general classes: incomposite, composite, and incomposite-composite.
< The incomposite numbers are those which have no divisor other than themselves and unity, such as 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, and so forth. For example, 7 is divisible only by 7, which goes into itself once, and unity, which goes into 7 seven times.
The composite numbers are those which are divisible not only by themselves and unity but also by some other number, such as 9, 15, 21, 25, 27, 33, 39, 45, 51, 57, and so forth. For example, 21 is divisible not only by itself and by unity, but also by 3 and by 7.
The incomposite-composite numbers are those which have no common divisor, although each of itself is capable of division, such as 9 and 25. For example, 9 is divisible by 3 and 25 by 5, but neither is divisible by the divisor of the other; thus they have no common divisor. Because they have individual divisors, they are called composite; and because they have no common divisor, they are called in, composite. Accordingly, the term incomposite-composite was created to describe their properties.
Even numbers are divided into three classes: evenly-even, evenly-odd, and oddly-odd.
The evenly-even numbers are all in duple ratio from unity; thus: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, and 1,024. The proof of the perfect evenly-even number is that it can be halved and the halves again halved back to unity, as 1/2 of 64 = 32; 1/2 of 32 = 16; 1/2 of 16 = 8; 1/2 of 8 = 4; 1/2 of 4 = 2; 1/2 of 2 = 1; beyond unity it is impossible to go.
The evenly-even numbers possess certain unique properties. The sum of any number of terms but the last term is always equal to the last term minus one. For example: the sum of the first and second terms (1+2) equals the third term (4) minus one; or, the sum of the first, second, third, and fourth terms (1+2+4+8) equals the fifth term (16) minus one.
In a series of evenly-even numbers, the first multiplied by the last equals the last, the second multiplied by the second from the last equals the last, and so on until in an odd series one number remains, which multiplied by itself equals the last number of the series; or, in an even series two numbers remain, which multiplied by each other give the last number of the series. For example: 1, 2, 4, 8, 16 is an odd series. The first number (1) multiplied by the last number (16) equals the last number (16). The second number (2) multiplied by the second from the last number (8) equals the last number (16). Being an odd series, the 4 is left in the center, and this multiplied by itself also equals the last number (16).
The evenly-odd numbers are those which, when halved, are incapable of further division by halving. They are formed by taking the odd numbers in sequential order and multiplying them by 2. By this process the odd numbers 1, 3, 5, 7, 9, 11 produce the evenly-odd numbers, 2, 6, 10, 14, 18, 22. Thus, every fourth number is evenly-odd. Each of the even-odd numbers may be divided once, as 2, which becomes two 1's and cannot be divided further; or 6, which becomes two 3's and cannot be divided further.
Another peculiarity of the evenly-odd numbers is that if the divisor be odd the quotient is always even, and if the divisor be even the quotient is always odd. For example: if 18 be divided by 2 (an even divisor) the quotient is 9 (an odd number); if 18 be divided by 3 (an odd divisor) the quotient is 6 (an even number).
The evenly-odd numbers are also remarkable in that each term is one-half of the sum of the terms on either side of it. For example:

THE SIEVE OF ERATOSTHENES. - Redrawn from Taylor's Theoretic Arithmetic.
This sieve is a mathematical device originated by Eratosthenes about 230 B.C. far the purpose of segregating the composite and incomposite odd numbers. Its use is extremely simple after the theory has once been mastered. All the odd numbers are first arranged in their natural order as shown in the second panel from the bottom, designated Odd Numbers. It will then be seen that every third number (beginning with 3) is divisible by 3, every fifth number (beginning with 5;) is divisible by 5, every seventh number (beginning with 7) is divisible by 7, every ninth number (beginning with 9) is divisible by 9, every eleventh number (beginning with 11) is divisible by 11, and so on to infinity. This system finally sifts out what the Pythagoreans called the "incomposite" numbers, or those having no divisor other than themselves and unity. These will be found in the lowest panel, designated Primary and Incomposite Numbers. In his History of Mathematics, David Eugene Smith states that Eratosthenes was one of the greatest scholars of Alexandria and was called by his admirers "the second Plato." Eratosthenes was educated at Athens, and is renowned not only for his sieve but for having computed, by a very ingenious method, the circumference and diameter of the earth. His estimate of the earth's diameter was only 50 miles less than the polar diameter accepted by modern scientists. This and other mathematical achievements of Eratosthenes, are indisputable evidence that in the third century before Christ the Greeks not only knew the earth to be spherical in farm but could also approximate, with amazing accuracy, its actual size and distance from both the sun and the moon. Aristarchus of Samos, another great Greek astronomer and mathematician, who lived about 250 B.C., established by philosophical deduction and a few simple scientific instruments that the earth revolved around the sun. While Copernicus actually believed himself to be the discoverer of this fact, he but restated the findings advanced by Aristarchus seventeen hundred years earlier.10 is one-half of the sum of 6 and 14; 18 is one-half the sum of 14 and 22; and 6 is one-half the sum of 2 and 10.
The oddly-odd, or unevenly-even, numbers are a compromise between the evenly-even and the evenly-odd numbers. Unlike the evenly-even, they cannot be halved back to unity; and unlike the evenly-odd, they are capable of more than one division by halving. The oddly-odd numbers are formed by multiplying the evenly-even numbers above 2 by the odd numbers above one. The odd numbers above one are 3, 5, 7, 9, 11, and so forth. The evenly-even numbers above 2 are 4, 8, 16, 32, 64, and soon. The first odd number of the series (3) multiplied by 4 (the first evenly-even number of the series) gives 12, the first oddly-odd number. By multiplying 5, 7, 9, 11, and so forth, by 4, oddly-odd numbers are found. The other oddly-odd numbers are produced by multiplying 3, 5, 7, 9, 11, and so forth, in turn, by the other evenly-even numbers (8, 16, 32, 64, and so forth). An example of the halving of the oddly-odd number is as follows: 1/2 of 12 = 6; 1/2 of 6 = 3, which cannot be halved further because the Pythagoreans did not divide unity.
Even numbers are also divided into three other classes: superperfect, deficient, and perfect.
- Superperfect or superabundant numbers are such as have the sum of their fractional parts greater than themselves. For example: 1/2 of 24 = 12; 1/4 = 6; 1/3 = 8; 1/6 = 4; 1/12 = 2; and 1/24 = 1. The sum of these parts (12+6+8+4+2+1) is 33, which is in excess of 24, the original number.
- Deficient numbers are such as have the sum of their fractional parts less than themselves. For example: 1/2 of 14 = 7; 1/7 = 2; and 1/14 = 1. The sum of these parts (7+2+1) is 10, which is less than 14, the original number.
- Perfect numbers are such as have the sum of their fractional parts equal to themselves. For example: 1/2 of 28 = 14; 1/4 = 7; 1/7 = 4; 1/14 = 2; and 1/28 = 1. The sum of these parts (14+7+4+2+1) is equal to 28.
The perfect numbers are extremely rare. There is only one between 1 and 10, namely, 6; one between 10 and 100, namely, 28; one between 100 and 1,000, namely, 496; and one between 1,000 and 10,000, namely, 8,128. The perfect numbers are found by the following rule: The first number of the evenly-even series of numbers (1, 2, 4, 8, 16, 32, and so forth) is added to the second number of the series, and if an incomposite number results it is multiplied by the last number of the series of evenly-even numbers whose sum produced it. The product is the first perfect number. For example: the first and second evenly-even numbers are 1 and 2. Their sum is 3, an incomposite number. If 3 be multiplied by 2, the last number of the series of evenly-even numbers used to produce it, the product is 6, the first perfect number. If the addition of the evenly-even numbers does not result in an incomposite number, the next evenly-even number of the series must be added until an incomposite number results. The second perfect number is found in the following manner: The sum of the evenly-even numbers 1, 2, and 4 is 7, an incomposite number. If 7 be multiplied by 4 (the last of the series of evenly-even numbers used to produce it) the product is 28, the second perfect number. This method of calculation may be continued to infinity.
Perfect numbers when multiplied by 2 produce superabundant numbers, and when divided by 2 produce deficient numbers.
The Pythagoreans evolved their philosophy from the science of numbers. The following quotation from Theoretic Arithmetic is an excellent example of this practice:
"Perfect numbers, therefore, are beautiful images of the virtues which are certain media between excess and defect, and are not summits, as by some of the ancients they were supposed to be. And evil indeed is opposed to evil, but both are opposed to one good. Good, however, is never opposed to good, but to two evils at one and the same time. Thus timidity is opposed to audacity, to both [of] which the want of true courage is common; but both timidity and audacity are opposed to fortitude. Craft also is opposed to fatuity, to both [of] which the want of intellect is common; and both these are opposed to prudence. Thus, too, profusion is opposed to avarice, to both [of] which illiberality is common; and both these are opposed to liberality. And in a similar manner in the other virtues; by all [of] which it is evident that perfect numbers have a great similitude to the virtues. But they also resemble the virtues on another account; for they are rarely found, as being few, and they are generated in a very constant order. On the contrary, an infinite multitude of superabundant and diminished numbers may be found, nor are they disposed in any orderly series, nor generated from any certain end; and hence they have a great similitude to the vices, which are numerous, inordinate, and indefinite."
THE TABLE OF THE TEN NUMBERS
(The following outline of the Pythagorean numbers is a paraphrase of the writings of Nicomachus, Theon of Smyrna, Proclus, Porphyry, Plutarch, Clement of Alexandria, Aristotle, and other early authorities.)
Monad--1--is so called because it remains always in the same condition--that is, separate from multitude. Its attributes are as follows: It is called mind, because the mind is stable and has preeminence; hermaphrodism, because it is both male and female; odd and even, for being added to the even it makes odd, and to the odd, even; God, because it is the beginning and end of all, but itself has neither beginning nor end; good, for such is the nature of God; the receptacle of matter, because it produces the duad, which is essentially material.
By the Pythagoreans monad was called chaos, obscurity, chasm, Tartarus, Styx, abyss, Lethe, Atlas, Axis, Morpho (a name for Venus), and Tower or Throne of Jupiter, because of the great power which abides in the center of the universe and controls the circular motion of the planers about itself. Monad is also called germinal reason, because it is the origin of all the thoughts in the universe. Other names given to it were: Apollo, because of its relation to the sun; Prometheus, because he brought man light; Pyralios, one who exists in fire; geniture, because without it no number can exist; substance, because substance is primary; cause of truth; and constitution of symphony: all these because it is the primordial one.
Between greater and lesser the monad is equal; between intention and remission it is middle; in multitude it is mean; and in time it is now, because eternity knows neither past nor future. It is called Jupiter, because he is Father and head of the gods; Vesta, the fire of the home, because it is located in the midst of the universe and remains there inclining to no side as a dot in a circle; form, because it circumscribes, comprehends, and terminates; love, concord, and piety, because it is indivisible. Other symbolic names for the monad are ship, chariot, Proteus (a god capable of changing his form), Mnemosyne, and Polyonymous (having many names).
The following symbolic names were given to the duad--2--because it has been divided, and is two rather than one; and when there are two, each is opposed to the other: genius, evil, darkness, inequality, instability, movability, boldness, fortitude, contention, matter, dissimilarity, partition between multitude and monad, defect, shapelessness, indefiniteness, indeterminate ness, harmony, tolerance, root, feet of fountain-abounding idea, top, Phanes, opinion, fallacy, alterity, diffidence, impulse, death, motion, generation, mutation, division, longitude, augmentation, composition, communion, misfortune, sustentation, imposition, marriage, soul, and science.
In his book, Numbers, W. Wynn Westcott says of the duad: "it was called 'Audacity,' from its being the earliest number to separate itself from the Divine One; from the 'Adytum of God-nourished Silence,' as the Chaldean oracles say."
As the monad is the father, so the duad is the mother; therefore, the duad has certain points in common with the goddesses Isis, Rhea (Jove's mother), Phrygia, Lydia, Dindymene (Cybele), and Ceres; Erato (one of the Muses); Diana, because the moon is forked; Dictynna, Venus, Dione, Cytherea; Juno, because she is both wife and sister of Jupiter; and Maia, the mother of Mercury.
While the monad is the symbol of wisdom, the duad is the symbol of ignorance, for in it exists the sense of separateness--which sense is the beginning of ignorance. The duad, however, is also the mother of wisdom, for ignorance--out of the nature of itself--invariably gives birth to wisdom.
The Pythagoreans revered the monad but despised the duad, because it was the symbol of polarity. By the power of the duad the deep was created in contradistinction to the heavens. The deep mirrored the heavens and became the symbol of illusion, for the below was merely a reflection of the above. The below was called maya, the illusion, the sea, the Great Void, and to symbolize it the Magi of Persia carried mirrors. From the duad arose disputes and contentions, until by bringing the monad between the duad, equilibrium was reestablished by the Savior-God, who took upon Himself the form of a number and was crucified between two thieves for the sins of men.
The triad--3--is the first number actually odd (monad not always being considered a number). It is the first equilibrium of unities; therefore, Pythagoras said that Apollo gave oracles from a tripod, and advised offer of libation three times. The keywords to the qualities of the triad are friendship, peace, justice, prudence, piety, temperance, and virtue. The following deities partake of the principles of the triad: Saturn (ruler of time), Latona, Cornucopiæ, Ophion (the great serpent), Thetis, Hecate, Polyhymnia (a Muse), Pluto, Triton, President of the Sea, Tritogenia, Achelous, and the Faces, Furies, and Graces. This number is called wisdom, because men organize the present, foresee the future, and benefit by the experiences of the fast. It is cause of wisdom and understanding. The triad is the number of knowledge--music, geometry, and astronomy, and the science of the celestials and terrestrials. Pythagoras taught that the cube of this number had the power of the lunar circle.
The sacredness of the triad and its symbol--the triangle--is derived from the fact that it is made up of the monad and the duad. The monad is the symbol of the Divine Father and the duad of the Great Mother. The triad being made of these two is therefore androgynous and is symbolic of the fact that God gave birth to His worlds out of Himself, who in His creative aspect is always symbolized by the triangle. The monad passing into the duad was thus capable of becoming the parent of progeny, for the duad was the womb of Meru, within which the world was incubated and within which it still exists in embryo.
The tetrad--4--was esteemed by the Pythagoreans as the primogenial number, the root of all things, the fountain of Nature and the most perfect number. All tetrads are intellectual; they have an emergent order and encircle the world as the Empyreum passes through it. Why the Pythagoreans expressed God as a tetrad is explained in a sacred discourse ascribed to Pythagoras, wherein God is called the Number of Numbers. This is because the decad, or 10, is composed of 1, 2, 3, and 4. The number 4 is symbolic of God because it is symbolic of the first four numbers. Moreover, the tetrad is the center of the week, being halfway between 1 and 7. The tetrad is also the first geometric solid.
Pythagoras maintained that the soul of man consists of a tetrad, the four powers of the soul being mind, science, opinion, and sense. The tetrad connects all beings, elements, numbers, and seasons; nor can anything be named which does not depend upon the tetractys. It is the Cause and Maker of all things, the intelligible God, Author of celestial and sensible good, Plutarch interprets this tetractys, which he said was also called the world, to be 36, consisting of the first four odd numbers added to the first four even numbers, thus:
Keywords given to the tetrad are impetuosity, strength, virility, two-mothered, and the key keeper of Nature, because the universal constitution cannot be without it. It is also called harmony and the first profundity. The following deities partook of the nature of the tetrad: Hercules, Mercury, Vulcan, Bacchus, and Urania (one of the Muses).
The triad represents the primary colors and the major planets, while the tetrad represents the secondary colors and the minor planets. From the first triangle come forth the seven spirits, symbolized by a triangle and a square. These together form the Masonic apron.
The pentad--5--is the union of an odd and an even number (3 and 2). Among the Greeks, the pentagram was a sacred symbol of light, health, and vitality. It also symbolized the fifth element--ether--because it is free from the disturbances of the four lower elements. It is called equilibrium, because it divides the perfect number 10 into two equal parts.
The pentad is symbolic of Nature, for, when multiplied by itself it returns into itself, just as grains of wheat, starting in the form of seed, pass through Nature's processes and reproduce the seed of the wheat as the ultimate form of their own growth. Other numbers multiplied by themselves produce other numbers, but only 5 and 6 multiplied by themselves represent and retain their original number as the last figure in their products.
The pentad represents all the superior and inferior beings. It is sometimes referred to as the hierophant, or the priest of the Mysteries, because of its connection with the spiritual ethers, by means of which mystic development is attained. Keywords of the pentad are reconciliation, alternation, marriage, immortality, cordiality, Providence, and sound. Among the deities who partook of the nature of the pentad were Pallas, Nemesis, Bubastia (Bast), Venus, Androgynia, Cytherea, and the messengers of Jupiter.
The tetrad (the elements) plus the monad equals the pentad. The Pythagoreans taught that the elements of earth, fire, air, and water were permeated by a substance called ether--the basis of vitality and life. Therefore, they chose the five-pointed star, or pentagram, as the symbol of vitality, health, and interpenetration.
It was customary for the philosophers to conceal the element of earth under the symbol of a dragon, and many of the heroes of antiquity were told to go forth and slay the dragon. Hence, they drove their sword (the monad) into the body of the dragon (the tetrad). This resulted in the formation of the pentad, a symbol of the victory of the spiritual nature over the material nature. The four elements are symbolized in the early Biblical writings as the four rivers that poured out of Garden of Eden. The elements themselves are under the control of the composite Cherubim of Ezekiel.
The Pythagoreans held the hexad--6--to represent, as Clement of Alexandria conceived, the creation of the world according to both the prophets and the ancient Mysteries. It was called by the Pythagoreans the perfection of all the parts. This number was particularly sacred to Orpheus, and also to the Fate, Lachesis, and the Muse, Thalia. It was called the form of forms, the articulation of the universe, and the maker of the soul.
Among the Greeks, harmony and the soul were considered to be similar in nature, because all souls are harmonic. The hexad is also the symbol of marriage, because it is formed by the union of two triangles, one masculine and the other feminine. Among the keywords given to the hexad are: time, for it is the measure of duration; panacea, because health is equilibrium, and the hexad is a balance number; the world, because the world, like the hexad, is often seen to consist of contraries by harmony; omnisufficient, because its parts are sufficient for totality (3 +2 + 1 = 6); unwearied, because it contains the elements of immortality.
By the Pythagoreans the heptad--7--was called "worthy of veneration." It was held to be the number of religion, because man is controlled by seven celestial spirits to whom it is proper for him to make offerings. It was called the number of life, because it was believed that human creatures born in the seventh month of embryonic life usually lived, but those born in the eighth month often died. One author called it the Motherless Virgin, Minerva, because it was nor born of a mother but out of the crown, or the head of the Father, the monad. Keywords of the heptad are fortune, occasion, custody, control, government, judgment, dreams, voices, sounds, and that which leads all things to their end. Deities whose attributes were expressed by the heptad were Ægis, Osiris, Mars, and Cleo (one of the Muses).
Among many ancient nations the heptad is a sacred number. The Elohim of the Jews were supposedly seven in number. They were the Spirits of the Dawn, more commonly known as the Archangels controlling the planets. The seven Archangels, with the three spirits controlling the sun in its threefold aspect, constitute the 10, the sacred Pythagorean decad. The mysterious Pythagorean tetractys, or four rows of dots, increasing from 1 to 4, was symbolic of the stages of creation. The great Pythagorean truth that all things in Nature are regenerated through the decad, or 10, is subtly preserved in Freemasonry through these grips being effected by the uniting of 10 fingers, five on the hand of each person.
The 3 (spirit, mind, and soul) descend into the 4 (the world), the sum being the 7, or the mystic nature of man, consisting of a threefold spiritual body and a fourfold material form. These are symbolized by the cube, which has six surfaces and a mysterious seventh point within. The six surfaces are the directions: north, east, south, west, up, and down; or, front, back, right, left, above, and below; or again, earth, fire, air, water, spirit, and matter. In the midst of these stands the 1, which is the upright figure of man, from whose center in the cube radiate six pyramids. From this comes the great occult axiom: "The center is the father of the directions, the dimensions, and the distances."
The heptad is the number of the law, because it is the number of the Makers of Cosmic law, the Seven Spirits before the Throne.
The ogdoad--8--was sacred because it was the number of the first cube, which form had eight corners, and was the only evenly-even number under 10 (1-2-4-8-4-2-1). Thus, the 8 is divided into two 4's, each 4 is divided into two 2's, and each 2 is divided into two 1's, thereby reestablishing the monad. Among the keywords of the ogdoad are love, counsel, prudence, law, and convenience. Among the divinities partaking of its nature were Panarmonia, Rhea, Cibele, Cadmæa, Dindymene, Orcia, Neptune, Themis, and Euterpe (a Muse).
The ogdoad was a mysterious number associated with the Eleusinian Mysteries of Greece and the Cabiri. It was called the little holy number. It derived its form partly from the twisted snakes on the Caduceus of Hermes and partly from the serpentine motion of the celestial bodies; possibly also from the moon's nodes.
The ennead--9--was the first square of an odd number (3x3). It was associated with failure and shortcoming because it fell short of the perfect number 10 by one. It was called the called the number of man, because of the nine months of his embryonic life. Among its keywords are ocean and horizon, because to the ancients these were boundless. The ennead is the limitless number because there is nothing beyond it but the infinite 10. It was called boundary and limitation, because it gathered all numbers within itself. It was called the sphere of the air, because it surrounded the numbers as air surrounds the earth, Among the gods and goddesses who partook in greater or less degree of its nature were Prometheus, Vulcan, Juno, the sister and wife of Jupiter, Pæan, and Aglaia, Tritogenia, Curetes, Proserpine, Hyperion, and Terpsichore (a Muse).
The 9 was looked upon as evil, because it was an inverted 6. According to the Eleusinian Mysteries, it was the number of the spheres through which the consciousness passed on its way to birth. Because of its close resemblance to the spermatozoon, the 9 has been associated with germinal life.
The decad--10--according to the Pythagoreans, is the greatest of numbers, not only because it is the tetractys (the 10 dots) but because it comprehends all arithmetic and harmonic proportions. Pythagoras said that 10 is the nature of number, because all nations reckon to it and when they arrive at it they return to the monad. The decad was called both heaven and the world, because the former includes the latter. Being a perfect number, the decad was applied by the Pythagoreans to those things relating to age, power, faith, necessity, and the power of memory. It was also called unwearied, because, like God, it was tireless. The Pythagoreans divided the heavenly bodies into ten orders. They also stated that the decad perfected all numbers and comprehended within itself the nature of odd and even, moved and unmoved, good and ill. They associated its power with the following deities: Atlas (for it carried the numbers on its shoulders), Urania, Mnemosyne, the Sun, Phanes, and the One God.
The decimal system can probably be traced back to the time when it was customary to reckon on the fingers, these being among the most primitive of calculating devices and still in use among many aboriginal peoples.
Suggestions for Further Reading
- The Pythagorean Sentences of Demophilus
- The Golden Verses of Pythagoras
- The Life and Philosophy of Pythagoras
- Secret Significance of Numbers and Pythagorean Mathematics
- Pythagoras, Pythagorean Wisdom, and Philosophy
- The Pythagorean Ethical Sentences From Stobaeus
- The Symbols of Pythagoras
- The Sevenfold Nature of Human Body
- The Historical Christ, The Story of Jesus From Occult Sources
- Thought Forms By Dr.Annie Besant
- Thoughts and Aphorisms of Sri Aurobindo
- Sri Aurobindo on Astrology
- Man and Battle for Life From The Essays on the Bhagavdgita by Sri Aurobindo
- Sri Aurobindo on Yoga
- Essay on rebirth by Sri Aurobindo
- The Reincarnating Soul by Sri Aurobindo
- An Essay on the Upanishads by Sri Aurobindo
- An Essay on the Vedas by Sri Aurobindo
- The Prayers and Meditations of the Divine Mother
- Writings and Quotationsof Jiddu Krishnamurthy
- Papaji Discourses
- Inspiarational Thoughts and Quotations
- Supreme Personality by Dr. Delmer Eugene Croft
- The Days and Nights of Brahma
- Life After Death
- The Seven Creations
- The Formation of Solar System
- The Zodiac and Its Antiquity
- Free EBooks and Texts on Greek Philosophy
- Essays On Dharma
- Esoteric Mystic Hinduism
- Introduction to Hinduism
- Hindu Way of Life
- Essays On Karma
- Hindu Rites and Rituals
- The Origin of The Sanskrit Language
- Symbolism in Hinduism
- Essays on The Upanishads
- Concepts of Hinduism
- Essays on Atman
- Hindu Festivals
- Spiritual Practice
- Right Living
- Yoga of Sorrow
- Happiness
- Mental Health
- Concepts of Buddhism
- General Essays
Source:THE SECRET TEACHINGS OF ALL AGES by Manly P. Hall [1928, copyright not renewed]